El número de oro

¡Buenas tardes! Hoy he decidido que sería buena idea explicaros ciertos aspectos sobre un número que, aunque lo tenemos presente de forma indirecta diariamente, la mayoría de vosotros no sabrá ni de su existencia.

El número áureo (también llamado número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) es un número irracional, representado por la letra griega φ (phi) en honor al escultor griego Fidias y cuyo valor es 1'61803398...

Os preguntaréis qué tiene que ver este número con la geometría, se trata de un número que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en las partes de un cuerpo, y en la naturaleza como relación entre cuerpos, en la morfología de diversos elementos tales como  las hojas de algunos árboles, proporciones humanas, etc.

A continuación, podéis ver este vídeo donde se explica brevemente en qué consiste este número y como se puede hallar el rectángulas con estas proporciones (rectángulo áureo).

Ya que tenéis una base de qué es este número os voy a contar cómo está presente en algunos de los objetos que estamos hartos de ver por casa.  Vosotros mismos podréis comprobar cómo se repite este número:

• En primer lugar, coged una tarjeta de crédito y medid sus proporciones (medida del largo y del ancho): os dará unas cantidades parecidas a 8,6 cm y 5,4 cm. Si dividís ambas cantidades os saldrá un número muy parecido al número áureo. Esto también lo podéis comprobar con otras tarjetas como son el DNI e incluso en un décimo de lotería.
• Ahora repetid los mismos pasos con un paquete de tabaco. Por casualidad no tendrá el mismo resultado, ¿no?.

• Pero si no tenéis ninguno de estos objetos en casa no os preocupéis,también podéis ver esta relación con el cuerpo humano. Leonardo Da Vinci reflejó la proporción áurea del cuerpo humano en el hombre de Vitruvio. Realizad el mismo proceso con algunas de estas medidas:

• La relación entre la altura de un ser humano y la altura de su ombligo.
• La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
• La relación entre la altura de la cadera y la altura de la rodilla.
• La relación entre el diámetro de la boca y el de la nariz.

• Además, también está presente en numerosas obras arquitectónicas como son la Torre Eiffel o el Partenón. El creador del Partenón fue Fidias (de ahí el nombre del número de oro) y como no podía ser menos la fachada del Partenón es un perfecto rectángulo de oro, pero además, hay otra serie de medidas en el edificio que también poseen proporciones áureas:

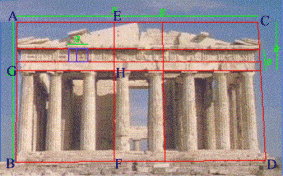En la foto están marcados los rectángulos áureos: ABCD, AEGH, AEBF, y sus simétricos. 

Además, la zona de las molduras (en color violeta) también está compuesta por rectángulos áureos.